4.3 Propiedades de vectores, combinación lineal, dependencia e independencia lineal.

Propiedades de los vectores

TEOREMA 1

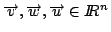Consideremos el vector yentonces

1.-
2.-
3.-
4.-
5.-
6.-
7.-
8.-
9.-

EJEMPLO

Combinación lineal

Un vector x se dice que es combinación lineal de un conjunto de vectores

si existe una forma de expresarlo como suma de parte o todos los vectores de A multiplicados cada uno de ellos por un coeficiente escalarde forma que:

Así, x es combinación lineal de vectores de A si podemos expresar como una suma de múltiplos de una cantidad finita de elementos de A.

Ejemplo: 2x + 3y − 2z = 0. Se dice que z es combinación lineal de x y de y, porque podemos escribir sin más que despejar la z. De la misma manera, despejando oportunamente, cada una de estas variables se podría expresar como combinación lineal de las otras dos.

En otras palabras, cuánto de cada vector del conjunto A necesito para que, cuando se combinen linealmente dichos elementos , pueda formar al vector en cuestión.

Dependencia e independencia lineal

Vectores linealmente dependientes

Varios vectores libres del plano se dice que son linealmente dependientes si hay una combinación lineal de ellos que es igual al vector cero, sin que sean cero todos los coeficientes de la combinación lineal.

Propiedades

1. Si varios vectores son linealmente dependientes, entonces al menos uno de ellos se puede expresar como combinación lineal de los demás.

También se cumple el reciproco: si un vector es combinación lineal de otros, entonces todos los vectores sonlinealmente dependientes.

2.Dos vectores del plano son linealmente dependientes si, y sólo si, son paralelos.

3.Dos vectores libres del plano = (u₁, u₂) y = (v₁, v₂) son linealmente dependientes si sus componentes son proporcionales.

Vectores linealmente independientes

Varios vectores libres son linealmente independientes si ninguno de ellos puede ser escrito con una combinación lineal de los restantes.

a₁ = a₂ = ··· = a_n = 0

Los vectores linealmente independientes tienen distinta dirección y sus componente no son proporcionales.

4.4 Base y dimensión de un espacio vectorial

Base.

Se llama base de un espacio (o subespacio) vectorial a un sistema generador de dicho espacio o subespacio, que sea a la vez linealmente independiente.

Propiedades de las bases

1.- Una base de S es un sistema generador minimal de S (lo más pequeño posible).

2.- Además es un conjunto independiente maximal dentro de S (lo más grande posible).

3.- Una base de S permite expresar todos los vectores de S como combinación lineal de ella, de manera única para cada vector.

Dimensión.

Todas las bases de un mismo espacio o subespacio tienen el mismo número de vectores. Se llama dimensión de dicho espacio o subespacio.

Por tanto, la dimensión es el máximo número de vectores independientes que podemos tener en el espacio o subespacio. En otras palabras, es el máximo rango que puede tener un Es también el rango de cualquier sistema generador de dicho espacio.

Propiedades de la dimensión.

• Significado físico de la dimensión: el espacio tiene dimensión 3, los planos dimensión 2, las rectas dimensión 1, el punto dimensión 0. El subespacio {0} es el único de dimensión 0.

• Número de parámetros libres en su forma paramétrica. (1 parámetro=recta, 2 parámetros= plano...)La dimensión de un subespacio en ℜⁿ, coincide con el

• Si S y T son subespacios y S está contenido en T, entonces dim S dim T.≤ Además, si se da la igualdad, dim S = dim T, entonces ambos espacios han de coincidir.
• El rango de una familia de vectores, es igual a la dimensión del subespacio que generan.

Teorema

Sea S un espacio o subespacio de dimensión m. Entonces,

• Si tenemos m vectores linealmente indep. en S, también serán sistema generador de S.

• Si tenemos m vectores que generan S, también serán linealmente independientes.

Por tanto, si tenemos un conjunto formado por tantos vectores como indica la dimensión, dichos vectores serán a la vez linealmente independientes y sistema generador, o bien ninguna de las dos cosas.

Así pues, para probar que son base, bastaría probar solamente una de las dos cosas: que son linealmente independientes, o que son sistema generador.

Esto solamente se puede aplicar cuando conocemos la dimensión del espacio y cuando tenemos tantos vectores como indica la dimensión.

Teorema.

En un espacio o subespacio de dimensión m,

• un conjunto de más de m vectores nunca puede ser linealmente independiente.

• un conjunto de menos de m vectores nunca puede ser sistema generador.

Así pues, por ejemplo, 3 vectores en ℜ² podrán ser o no sistema generador de ℜ², pero nunca podrán ser linealmente independientes.

Del mismo modo, 2 vectores en ℜ³ podrán ser linealmente independientes o no, pero nunca serán sistema generador de ℜ³ (aunque sí podrán serlo de un subespacio más pequeño).