4.5 Espacio vectorial con producto interno y sus propiedades
Definición. El espacio vectorial complejo V se conoce como un espacio con producto interior si para cualquier par de vectores u y v en V, existe un único número complejo (u, v), llamado el producto interior de u y v, tal que si u, v y w están en V y si α ∈ C, entonces
Propiedades
i. (v, v) ≥ 0
ii. (v, v) = 0 si y sólo si v = 0.
iii, (u, v +w) = (u, v)+ (u, w)
iv. (u + v, w) = (u, w)+(v, w)
v. (u, v) = (v, u)
vi. (αu, v) = α(u, v)
vii. (u, αv) = α(u, v)
La barra en las condiciones (v) y (vii) denota el conjugado complejo.
4.6 cambio de base, base ortonormal, proceso de ortonormalización Gram-Schmidt.
Cambio de base
El cambio de base consiste en conocidas las coordenadas de un vector respecto a una base B, encontrar las coordenadas de dicho vector con respecto a otra base B’.
TEOREMA 4.10 (La inversa de la matriz de transición).
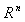 , entonces P es invertible y la matriz de transición de B’a B es
, entonces P es invertible y la matriz de transición de B’a B es Base ortonormal
En álgebra lineal, una base ortonormal de un espacio prehilbertiano V (es decir, un espacio vectorial con producto interno) o, en particular, de un espacio de Hilbert H, es un conjunto de elementos cuyo span es denso en el espacio, en el que los elementos son mutuamente ortogonales y normales, es decir, de magnitud unitaria. Una base ortogonal satisface las mismas condiciones, salvo la de magnitud unitaria; es muy sencillo transformar una base ortogonal en una base ortonormal mediante el producto por un escalar apropiado y de hecho, esta es la forma habitual en la que se obtiene una base ortonormal: por medio de una base ortogonal.
Así, una base ortonormal es una base ortogonal, en la cual la norma de cada elemento que la compone es unitaria.
Estos conceptos son importantes tanto para espacios de dimensión finita como de dimensión infinita. Para espacios de dimensión finita, la condición de span denso es la misma que la de 'span', como se usa en álgebra lineal.
Una base ortonormal por lo general no es una "base", es decir, en general no es posible escribir a cada elemento del espacio como una combinación lineal de un número finito de elementos de la base ortonormal. En el caso de dimensión infinita, esta distinción cobra importancia: la definición dada requiere solo que el span de una base ortonormal sea densa en el espacio vectorial, y no que iguale al espacio entero.
Una base ortonormal de un espacio vectorial V no tiene sentido si el espacio no posee un producto interno. Un Espacio de Banach no tendrá una base ortonormal a no ser que sea unespacio de Hilbert.
Proceso de ortonormalización Gram – Schmidt
El proceso de ortogonalización de Gram–Schmidt de álgebra lineal es un proceso utilizado en matemática y análisis numérico, para ortogonalizar un conjunto de vectores en un espacio prehilbertiano, más comúnmente el espacio euclídeo Rn. Ortogonalización en este contexto significa lo siguiente: comenzamos con vectores v1,…, vk los cuales son linealmente independientes y queremos encontrar mutuamente vectores ortogonales u1, …, uk los cuales generan el mismo subespacio que los vectores v1, …, vk.
Este proceso lleva el nombre en honor a Jørgen Pedersen Gram y Erhard Schmidt. Proceso de Gram–Schmidt Definimos el operador proyección condonde los corchetes angulares representan el producto interior, proyecta el vector v ortogonalmente en el vector u. Antes de ver el proceso, debemos comprender el porqué de la definición de proyección. Si recordamos la definición de producto escalar, tenemos para el caso del numerador, módulo de u por módulo de v por el coseno del ángulo que forman.
En el denominador tenemos módulo de u por módulo de u, ya que el coseno sería 1. Si separamos los dos módulos de u en el denominador, vemos que a la izquierda tenemos únicamente “módulo de v * cos (ángulo que forman)”, lo que nos da claramente el módulo del vector proyección. Teniendo el módulo del vector proyección lo único que debemos hacer es asignarle una dirección, cosa que hacemos multiplicándolo por u/módulo(u), lo que es el vector de módulo 1 con dirección u (el vector unitario).




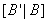


SuReYmA. Gracias por la información, esta muy completa...
ResponderEliminarbuena amiga
ResponderEliminarme ayudooo muchoooo graciassss SuReYmA ;)
ResponderEliminarsiii muy completa y menos enredosa q las demas paginas
ResponderEliminarTE AMOOOOOOOOOOOOOOOOOOOO TU INFORMACION ME AYUDO MUCHISIMO =)
ResponderEliminarGRACIAS POR LA INFORMACION ME SALVASTE GRACIAS ;)
ResponderEliminarjujujjujuju que padre gracias mil!
ResponderEliminar