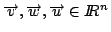UNIDAD IV: ESPACIOS VECTORIALES

4.1 Definición de espacio vectorial y sus propiedades.

Un espacio vectorial (o espacio lineal) es el objeto básico de estudio en la rama de la matemática llamada álgebra lineal. A los elementos de los espacios vectoriales se les llama vectores. Sobre los vectores pueden realizarse dos operaciones: escalarse (multiplicarlos por un escalar) y sumarse. Estas dos operaciones se tienen que ceñir a un conjunto de axiomas que generalizan las propiedades comunes de las tuplas de números reales así como de los vectores en el espacio euclídeo. Un concepto importante es el de dimensión.

Históricamente, las primeras ideas que condujeron a los espacios vectoriales modernos se remontan al siglo XVII: geometría analítica, matrices ysistemas de ecuaciones lineales. La primera formulación moderna y axiomática se debe a Giuseppe Peano, a finales del siglo XIX. Los siguientes avances en la teoría de espacios vectoriales provienen del análisis funcional, principalmente de los espacios de funciones. Los problemas de Análisis funcional requerían resolver problemas sobre la convergencia. Esto se hizo dotando a los espacios vectoriales de una adecuada topología, permitiendo tener en cuenta cuestiones de proximidad y continuidad. Estos espacios vectoriales topológicos, en particular los espacios de Banach y los espacios de Hilbert tienen una teoría más rica y complicada.

Los espacios vectoriales tienen aplicaciones en otras ramas de la matemática, la ciencia y la ingeniería. Se utilizan en métodos como las series de Fourier, que se utiliza en las rutinas modernas de compresión de imágenes y sonido, o proporcionan el marco para resolver ecuaciones en derivadas parciales. Además, los espacios vectoriales proporcionan una forma abstracta libre de coordenadas de tratar con objetos geométricos y físicos, tales como tensores, que a su vez permiten estudiar las propiedades locales de variedades mediante técnicas de linealización.

Propiedades del espacio vectorial.

Hay una serie de propiedades que se demuestran fácilmente a partir de los axiomas del espacio vectorial. Algunas de ellas se derivan de la teoría elemental de grupos, aplicada al grupo (aditivo) de vectores: por ejemplo, el vector nulo 0 Є V, y el opuesto -v de un vector v son únicos. Otras propiedades se pueden derivar de la propiedad distributiva, por ejemplo, la multiplicación por el escalar cero da el vector nulo y ningún otro escalar multiplicado por un vector da cero:

Propiedad	Significado
Unicidad del vector nulo
Unicidad del opuesto de un vector
Producto por el escalar cero	0 v = 0. El 0 es el único escalar que cumple esta propiedad.
Producto de un escalar por el vector nulo	a 0 = 0
Opuesto del producto de un vector por un escalar	- (a v) = (-a) v = a (-v)

4.2 Definición de subespacio de un espacio vectorial y sus propiedades.

Subespacio vectorial

Definición

Sean (V,+,K,*) un espacio vectorial y S un subconjunto de V. S es subespacio vectorial de V si (S,+,K,*) es espacio vectorial en sí mismo, siendo + y * las mismas operaciones definidas en V.

Criterio de subespacio

El criterio para la verificación de que S es subespacio de V, es que ambas operaciones (+ entre elementos del conjunto S y * con escalares del cuerpo K) sean cerradas, es decir, den como resultado elementos que también pertenezcan a S.

Propiedades

Un espacio vectorial es un conjunto no vacío que cumple con estas tres condiciones:

1) El Punto Origen pertenece al conjunto. Ej: (0,0,0).

2) Sea K un número real y {v} un vector que pertenece al conjunto entonces K.v también pertenece al conjunto.

3) Sean {u} y {v} dos vectores que pertenecen al conjunto entonces u+v también pertenece al conjunto.

Si estos tres axiomas se cumplen entonces el conjunto es un subespacio.

4.3 Propiedades de vectores, combinación lineal, dependencia e independencia lineal.

Propiedades de los vectores

TEOREMA 1

Consideremos el vector yentonces

1.-
2.-
3.-
4.-
5.-
6.-
7.-
8.-
9.-

EJEMPLO

Combinación lineal

Un vector x se dice que es combinación lineal de un conjunto de vectores

si existe una forma de expresarlo como suma de parte o todos los vectores de A multiplicados cada uno de ellos por un coeficiente escalarde forma que:

Así, x es combinación lineal de vectores de A si podemos expresar como una suma de múltiplos de una cantidad finita de elementos de A.

Ejemplo: 2x + 3y − 2z = 0. Se dice que z es combinación lineal de x y de y, porque podemos escribir sin más que despejar la z. De la misma manera, despejando oportunamente, cada una de estas variables se podría expresar como combinación lineal de las otras dos.

En otras palabras, cuánto de cada vector del conjunto A necesito para que, cuando se combinen linealmente dichos elementos , pueda formar al vector en cuestión.

Dependencia e independencia lineal

Vectores linealmente dependientes

Varios vectores libres del plano se dice que son linealmente dependientes si hay una combinación lineal de ellos que es igual al vector cero, sin que sean cero todos los coeficientes de la combinación lineal.

Propiedades

1. Si varios vectores son linealmente dependientes, entonces al menos uno de ellos se puede expresar como combinación lineal de los demás.

También se cumple el reciproco: si un vector es combinación lineal de otros, entonces todos los vectores sonlinealmente dependientes.

2.Dos vectores del plano son linealmente dependientes si, y sólo si, son paralelos.

3.Dos vectores libres del plano = (u₁, u₂) y = (v₁, v₂) son linealmente dependientes si sus componentes son proporcionales.

Vectores linealmente independientes

Varios vectores libres son linealmente independientes si ninguno de ellos puede ser escrito con una combinación lineal de los restantes.

a₁ = a₂ = ··· = a_n = 0

Los vectores linealmente independientes tienen distinta dirección y sus componente no son proporcionales.

4.4 Base y dimensión de un espacio vectorial

Base.

Se llama base de un espacio (o subespacio) vectorial a un sistema generador de dicho espacio o subespacio, que sea a la vez linealmente independiente.

Propiedades de las bases

1.- Una base de S es un sistema generador minimal de S (lo más pequeño posible).

2.- Además es un conjunto independiente maximal dentro de S (lo más grande posible).

3.- Una base de S permite expresar todos los vectores de S como combinación lineal de ella, de manera única para cada vector.

Dimensión.

Todas las bases de un mismo espacio o subespacio tienen el mismo número de vectores. Se llama dimensión de dicho espacio o subespacio.

Por tanto, la dimensión es el máximo número de vectores independientes que podemos tener en el espacio o subespacio. En otras palabras, es el máximo rango que puede tener un Es también el rango de cualquier sistema generador de dicho espacio.

Propiedades de la dimensión.

• Significado físico de la dimensión: el espacio tiene dimensión 3, los planos dimensión 2, las rectas dimensión 1, el punto dimensión 0. El subespacio {0} es el único de dimensión 0.

• Número de parámetros libres en su forma paramétrica. (1 parámetro=recta, 2 parámetros= plano...)La dimensión de un subespacio en ℜⁿ, coincide con el

• Si S y T son subespacios y S está contenido en T, entonces dim S dim T.≤ Además, si se da la igualdad, dim S = dim T, entonces ambos espacios han de coincidir.
• El rango de una familia de vectores, es igual a la dimensión del subespacio que generan.

Teorema

Sea S un espacio o subespacio de dimensión m. Entonces,

• Si tenemos m vectores linealmente indep. en S, también serán sistema generador de S.

• Si tenemos m vectores que generan S, también serán linealmente independientes.

Por tanto, si tenemos un conjunto formado por tantos vectores como indica la dimensión, dichos vectores serán a la vez linealmente independientes y sistema generador, o bien ninguna de las dos cosas.

Así pues, para probar que son base, bastaría probar solamente una de las dos cosas: que son linealmente independientes, o que son sistema generador.

Esto solamente se puede aplicar cuando conocemos la dimensión del espacio y cuando tenemos tantos vectores como indica la dimensión.

Teorema.

En un espacio o subespacio de dimensión m,

• un conjunto de más de m vectores nunca puede ser linealmente independiente.

• un conjunto de menos de m vectores nunca puede ser sistema generador.

Así pues, por ejemplo, 3 vectores en ℜ² podrán ser o no sistema generador de ℜ², pero nunca podrán ser linealmente independientes.

Del mismo modo, 2 vectores en ℜ³ podrán ser linealmente independientes o no, pero nunca serán sistema generador de ℜ³ (aunque sí podrán serlo de un subespacio más pequeño).