5.2 Ejemplos de transformaciones lineales (Reflexión, Dilatación, Contracción, Rotación).

Reflexión

Algunas orientaciones deseables para los objetos tridimensionales no pueden ser obtenidas usando solamente giros. Con la reflexión se consigue un efecto "espejo", de modo que los objetos se ven reflejados en un plano.

Cuando la reflexión se hace sobre uno de los planos ortogonales (x = 0, o y = 0, o bien z = 0) la matriz de transformación es sencilla, pues es similar a la matriz identidad, aunque siendo –1 el elemento que representa a la coordenada que es nula en el plano de reflexión. Así, las matrices de reflexión para los planos XY, XZ e YZ son

Cuando se quiera una reflexión sobre un plano cualquiera, el proceso se complica notablemente. La técnica utilizada es similar a la del giro sobre eje arbitrario. En este caso, inicialmente se requiere definir un punto en el plano, y la normal al plano en ese punto.

El proceso de reflexión se resume en los siguientes puntos:

• Trasladar el punto establecido del plano al origen de coordenadas

• Realizar los giros oportunos para hacer coincidir el vector normal al plano de reflexión con uno de los ejes de coordenadas; así el problema se reduce a una simple reflexión sobre alguno de los planos del sistema de referencia.

Por ejemplo, si el eje escogido es el Z, el plano de reflexión sería el XY.

• Realizar la reflexión sobre el plano seleccionado

• Aplicar las transformaciones inversas para devolver el plano de reflexión a su posición original.

La matriz neta podría ser, por ejemplo, el resultado de la composición de las matrices [M]= [T]⋅ [G ]⋅ [G ]⋅ [R ]⋅ [G ]−1 ⋅ [G ]−1 ⋅[T]−1 x y z y x , si se opta por realizar las transformaciones para alinear el vector normal con el eje Z. En tal caso, la matriz de reflexión a utilizar sería la Rz.

Rotación

Otro tipo común de transformación en el plano es la rotación o giro en torno a cualquier punto en el plano. Nos interesan principalmente las rotaciones en tormo al origen. Rotación en el plano: La transformación 𝑅𝜃:𝑅2→𝑅2 se define por

y hace girar cada vector, θ rad en sentido contrario al de las manecillas del reloj en torno al origen.

Por ejemplo, calcularemos la imagen de (1,1) para �𝜃=𝜋/2.

Rotación en torno al origen

COMPRESIONES-EXPANSIONES

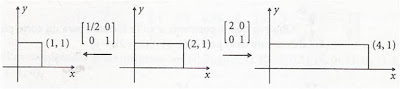
Las compresiones y expansiones son escalamientos a lo largo de los ejes coordenados. Con mas precisión: para �CC>𝑐>0, la transformación �𝐶𝑥 𝑥, =(𝑐𝑥,𝑦) escala las coordenadas x en un factor de c, dejando inalteradas a las coordenadas y. Si 0<𝑐<1 se trata de una compresión en la dirección del eje x positivo. Si �𝑐>1, se refiere a una expansión. También se tienen compresiones y expansiones a lo largo del eje y, expresadas por �𝐶𝑦 𝑥, = 𝑐,𝑦 para �𝑐>0.

Compresión y estiramiento a lo largo del eje x.

Otro tipo son los escalamiento simultáneos a lo largo de los ejes x y y, como 𝐶𝑥𝑦 𝑥, = 𝑐𝑥,𝑦 con factores de escala �𝑐>0 y 𝑑>0 a lo largo de las direcciones x y y.

Escalamiento a lo largo de los ejes x y y.

Tanto �𝐶𝑥 como �𝐶𝑦 y 𝐶𝑥𝑦 son transformaciones matriciales, con sus respectivas matrices

CORTES

Un corte o deslizamiento a lo largo del eje x es una transformación de la forma 𝑆𝑥 𝑥,𝑦 =(𝑥+𝑐𝑦,𝑦)

En otras palabras, cada punto se mueve a lo largo de la dirección x una cantidad proporcional a la distancia al eje x. También hay cortes a lo largo del eje y:

�𝑆𝑦 𝑥,𝑦 =(𝑥,𝑐𝑥+𝑦)

𝑆𝑥 y 𝑆𝑦 son transformaciones matriciales cuyas matrices son

Deslizamiento a lo largo del eje x.